# 다익스트라 알고리즘 (Dijkstra's algorithm)
다익스트라 알고리즘은 한 노드에서 다른 모든 노드까지의 최단 경로를 찾는 알고리즘이다.
모든 간선의 값이 0 이상일 때, 즉 음의 간선이 없을 때에만 사용할 수 있는 알고리즘이다.
가장 비용이 적은 노드를 선택해 임의의 과정을 반복하기 때문에 그리디 알고리즘으로 분류된다.
다익스트라 알고리즘은 아래와 같은 순서로 진행된다.
- 출발 노드 선택
- 최단 거리 테이블을 초기화
- 방문하지 않은 노드 중 최단 거리가 가장 짧은 노드를 선택
- 선택한 노드에서 다른 노드로 가는 비용 계산 및 테이블 업데이트
- 종료 조건까지 3, 4번 반복
3번에서 최단 거리가 가장 짧은 노드를 선택하는 방법에 따라 시간 복잡도가 달라진다.
최단 거리 테이블을 단순히 선형 탐색하는 방법으로 구현 시 O(V2)의 시간 복잡도를 가지나,
최소 힙을 활용한 우선순위 큐(priority queue)를 사용하면 O(ElogV)로 시간 복잡도를 개선할 수 있다. (E: 간선의 개수)
우선순위 큐는 FIFO인 일반 큐와는 다르게 우선순위가 높은 값 먼저 삭제한다는 특징을 가지고 있다.
최소 힙은 가장 작은 값이 먼저 삭제되는 특징이 있으므로 비용이 적은 노드를 선택해 방문해야 하는 다익스트라 알고리즘에 활용하기 매우 적합하다.
# Process
Priority queue를 이용한 방법을 살펴볼 것이다.
큐가 비어있을 때 종료된다.
가장 먼저 최단 거리 테이블을 무한으로 초기화한다.

출발 노드의 거리를 0으로 설정하고 그 정보를 큐에 넣는다. 해당 노드는 방문 처리 한다.

(반복 1)
큐에서 노드를 꺼내고 이와 연결된 노드 중 방문하지 않은 다른 노드에 대해 아래 작업을 진행한다.
(꺼낸 노드의 거리 값 + 간선의 비용)이 (연결된 노드의 최단 거리 테이블 값) 보다 작은 경우 큐에 넣고 테이블을 업데이트 한다.

(반복 2)
반복 1의 동작을 수행한다.
4번 노드에서 2번 노드로 가는 경로는 비용이 4로 기존 2번 노드의 비용보다 크므로 무시한다.

(반복 3)
반복 1의 동작을 수행한다.
노드 2에서 노드 5로의 비용은 3으로 기존 노드 5의 거리 값과 같으므로 무시한다.

(반복 4)
연결된 노드가 없으므로 할 작업이 없다.

(반복 5)
이미 방문 처리된 5번이 다시 pop 되었으며 따로 해주어야 할 작업은 없다.
이런 경우에 pop 된 거리 값은 최소 거리 테이블의 거리 값보다 크다.
그 이유는 priority queue의 규칙에 따라 더 작은 거리 값을 가지는 경우가 먼저 pop 되고 방문 처리되기 때문이다.
이러한 경우를 방지하고자 구현 코드에서는 pop한 거리 값이 테이블 거리 값보다 크면 continue 처리한다.

(반복 6)
연결된 노드가 없으므로 할 작업이 없다.
큐가 비었으므로 작업이 종료된다.
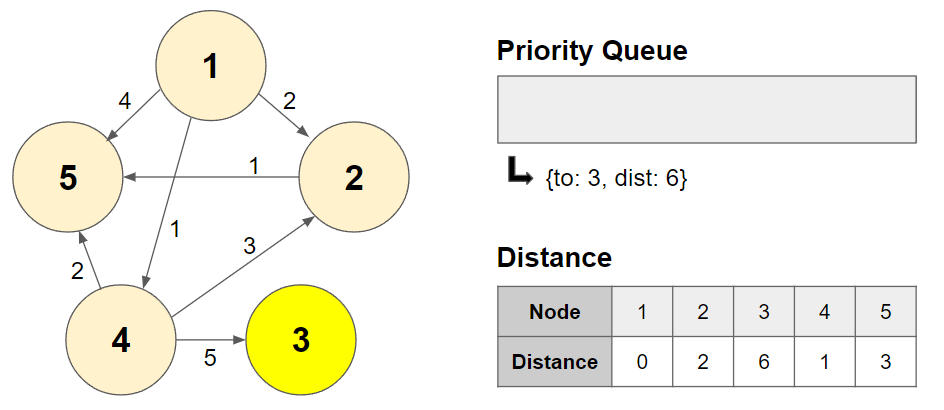
이러한 일련의 과정이 끝난 후 최소 거리 테이블을 살펴보면 1번 노드에서 각 노드까지의 최소 경로 비용을 알 수 있다.
만약 도달할 수 없는 경우에는 INF로 값이 나타날 것이다.
# JavaScript로 구현
많은 언어에서 힙을 이용한 priority queue를 지원하나, JavaScript에는 해당되지 않는다.
따라서 힙을 이용하기 위해선 직접 구현하여 사용해야 한다.
JavaScript에서 힙 직접 구현하기는 아래 링크를 참고.
https://chamdom.blog/heap-using-js/
이번에는 코드를 조금 더 단순화하기 위해 heap 대신 JS sort를 활용한 priority queue 구현하였다.
일단 이 방법으로 프로그래머스에서 테스트를 해 본 결과 딱히 시간 초과가 걸리거나 하지는 않아 보인다.
힙을 이용하는 것은 언젠가 다음 기회에...
const INF = Number.MAX_SAFE_INTEGER;
class PriorityQueue {
constructor() { this.queue = []; }
push(input) {
this.queue.push(input);
this.queue.sort((a, b) => a.dist - b.dist);
}
pop() { return this.queue.shift(); }
size() { return this.queue.length; }
}
function dijkstra(adjList, start) {
const priQue = new PriorityQueue();
const distance = new Array(adjList.length).fill(INF);
// 첫 번째 노드 처리
priQue.push({ to: start, dist: 0 });
distance[start] = 0;
// 반복
while(priQue.size()) {
let { to: curNode, dist: curDist } = priQue.pop();
if (curDist > distance[curNode]) continue; // 반복 5 케이스
adjList[curNode].forEach(next => {
let [nextNode, nextDist] = next;
let cost = curDist + nextDist;
if (cost < distance[nextNode]) {
distance[nextNode] = cost;
priQue.push({to: nextNode, dist: cost});
}
});
}
return distance;
}
Process의 예시를 실행하면 다음과 같다.
const n = 5; // 노드 개수
const adjList = new Array(n + 1);
adjList[0] = []; // 주어진 노드 번호를 그대로 사용하기 위해 index 0는 무시
adjList[1] = [[2, 2], [4, 1], [5, 4]];
adjList[2] = [[5, 1]];
adjList[3] = [];
adjList[4] = [[2, 3], [3, 5], [5, 2]];
adjList[5] = [];
const result = dijkstra(adjList, 1);
console.log(result.slice(1)); // 불필요한 0번째 index 제외하고 출력
// 결과: [ 0, 2, 6, 1, 3 ]※ adjList[n]: n번 node에 연결된 간선 정보를 담은 배열
ex) adjList[1][0]은 (1번 노드) --> (2번 노드)의 간선 비용이 2라는 의미
adjList[1][1]은 (1번 노드) --> (4번 노드)의 간선 비용이 1라는 의미
adjList[4][1]은 (4번 노드) --> (3번 노드)의 간선 비용이 5라는 의
'Algorithms' 카테고리의 다른 글
| 순열과 조합 (with JavaScript) (0) | 2023.08.24 |
|---|---|
| 플로이드 워셜 알고리즘 (with JavaScript) (0) | 2023.07.20 |
| Dynamic Programming (with JavaScript) (0) | 2023.07.17 |
| Binary Search (with JavaScript) (0) | 2023.07.14 |
| Counting Sort (with JavaScript) (0) | 2023.07.14 |
