# 크루스칼 알고리즘(Kruskal Algorithm)
크루스칼 알고리즘은 최소 신장 트리 (Minimum Spanning Tree)를 만드는데 사용하는 알고리즘으로 그리디 알고리즘으로 분류된다.
비용이 작은 간선을 선택하며 서로소 집합 자료구조를 이용해 사이클이 발생하지 않도록 처리하는 방법이다.
이를 통해 불필요한 간선(사이클이 발생하는 간선)이 선택되지 않으면서도 간선 비용의 합이 가장 작은 신장 트리를 만들 수 있다.
모든 간선을 정렬하고 순회하기 때문에 간선의 수가 적은 그래프에서 활용하기에 적합하다.
간선의 수가 노드에 비해 훨씬 많다면 프림 알고리즘의 사용을 고려하자.
서로소 집합을 이용한 사이클 판별
서로소 집합을 통해 사이클인지 확인하는 방법은 간선 양쪽 노드의 find 연산 결과가 같은지 확인하는 것이다.

위 그래프에서 find(2) === find(3) === 0이므로 간선 (2, 3)은 사이클을 발생시키는 것을 알 수 있다.
반면 find(1) !== find(2)이므로 간선 (1, 2)는 사이클을 유발하지 않음을 알 수 있다.
# Process
1. 간선을 비용이 오름차순이 되도록 정렬한다.
2. 비용이 작은 간선부터 서로소 집합을 이용해 사이클이 발생하는지 체크하고 사이클이 발생하지 않으면 신장 트리에 추가한다.
Ex.
크루스칼 알고리즘을 이용하여 아래와 같은 그래프의 최소 신장 트리를 구하는 과정이다.

1. 가장 작은 비용을 가진 0-3 간선을 선택한다. 사이클이 아니므로 신장 트리에 추가한다.

2. 그 다음 작은 비용을 가진 1-2 간선을 선택한다. 사이클이 아니므로 신장 트리에 추가한다.

3. 그 다음 작은 비용을 가진 0-2 간선을 선택한다. 사이클이 아니므로 신장 트리에 추가한다.

4. 그 다음 작은 비용을 가진 0-1 간선을 선택한다. 사이클이므로 신장 트리에 추가하지 않는다.
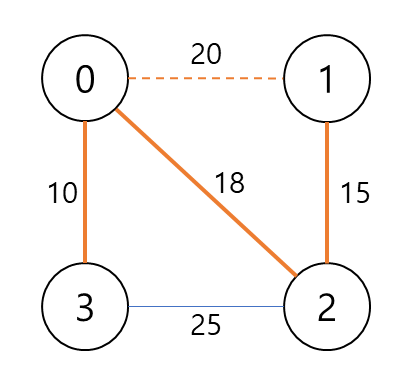
5. 그 다음 작은 비용을 가진 2-3 간선을 선택한다. 사이클이므로 신장 트리에 추가하지 않는다.

'N' 모양의 최소 신장 트리가 완성되었다.
최소 신장 트리의 총 비용은 43이다.
# 구현
// n: node의 개수
// edges: 모든 edge의 정보를 담은 배열
function kruskal(n, edges) {
// 비용에 따라 오름차순으로 정렬
edges.sort((a, b) => a.cost - b.cost);
// 서로소 집합을 위한 parent 배열
let parent = new Array(n).fill().map((_val, idx) => idx);
let totalCost = 0;
edges.forEach((edge) => {
// 서로소가 아닌 경우 신장 트리에 추가
if (find(parent, edge.from) !== find(parent, edge.to)) {
union(parent, edge.from, edge.to);
totalCost += edge.cost;
}
});
return totalCost;
}
function find(parent, x) {
if (parent[x] !== x) {
parent[x] = find(parent, parent[x]);
}
return parent[x];
}
function union(parent, a, b) {
let pA = find(parent, a);
let pB = find(parent, b);
if (pA < pB) parent[pB] = pA;
else parent[pA] = pB;
}
const edges = [
{ from: 0, to: 1, cost: 20 },
{ from: 0, to: 2, cost: 18 },
{ from: 0, to: 3, cost: 10 },
{ from: 1, to: 2, cost: 15 },
{ from: 2, to: 3, cost: 25 },
];
console.log(kruskal(4, edges));
// 43
'Algorithms' 카테고리의 다른 글
| 누적 합 (feat. 파괴되지 않는 건물) - 1 (0) | 2023.09.05 |
|---|---|
| 위상 정렬 (with JavaScript) (0) | 2023.09.02 |
| 서로소 집합 (with JavaScript) (0) | 2023.09.02 |
| 순열과 조합 (with JavaScript) (0) | 2023.08.24 |
| 플로이드 워셜 알고리즘 (with JavaScript) (0) | 2023.07.20 |
