# 위상 정렬 (Topology Sort)
위상 정렬은 순서가 정해져 있는 작업을 차례대로 수행해야 할 때 사용할 수 있는 알고리즘이다.
비순환 유향 그래프에서 사용할 수 있다.
진입 차수(indegree), 즉 자신으로 들어오는 간선의 수가 0인 노드부터 차례대로 제거해나가며 순서를 정한다.
# Process
- 진입 차수가 0인 노드를 큐에 담는다.
- 큐가 빌 때까지 큐에서 원소를 꺼내고 해당 노드에 연결된 간선을 제거한다.
- 새롭게 진입 차수가 0이 된 노드를 큐에 담는다.
Ex.
대표적인 예시로 선수과목 있는 수강 계획 순서를 정할 때 사용할 수 있다.

0 ~ 5번의 과목이 있고 각 과목은 자신을 가리키는 선수 과목을 모두 들은 후에야 수강할 수 있다고 하자.
예를 들어 4번 과목은 1, 2번 과목을 모두 수강해야 들을 수 있다.
1. 진입 차수가 0인 0번 노드를 큐에 담는다.

2. 노드 0을 꺼내고 연결된 간선을 제거한다. 새롭게 진입 차수가 0이 된 1, 2번 노드를 큐에 담는다.
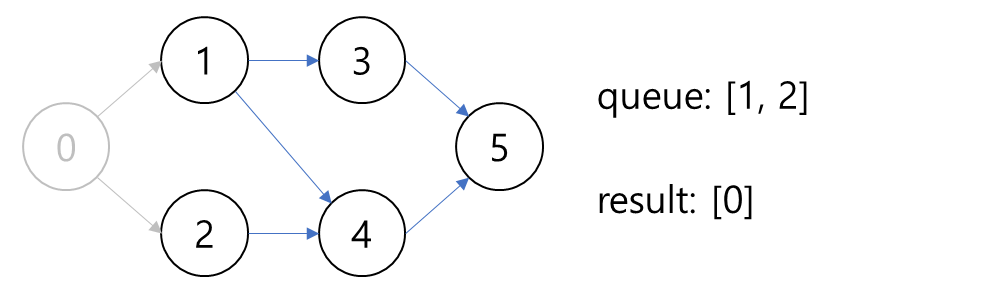
3. 노드 1를 꺼내고 연결된 간선을 제거한다. 새롭게 진입 차수가 0이 된 3번 노드를 큐에 담는다.

4. 노드 2을 꺼내고 연결된 간선을 제거한다. 새롭게 진입 차수가 0이 된 4번 노드를 큐에 담는다.

5. 노드 3를 꺼내고 연결된 간선을 제거한다. 새롭게 진입 차수가 0이 된 노드는 없다.
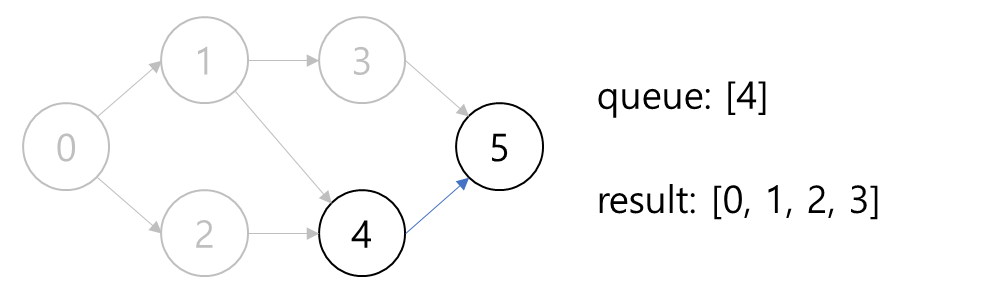
6. 노드 4를 꺼내고 연결된 간선을 제거한다. 새롭게 진입 차수가 0이 된 5번 노드를 큐에 담는다.

7. 노드 5을 꺼낸다. 큐가 비었으므로 마무리한다.
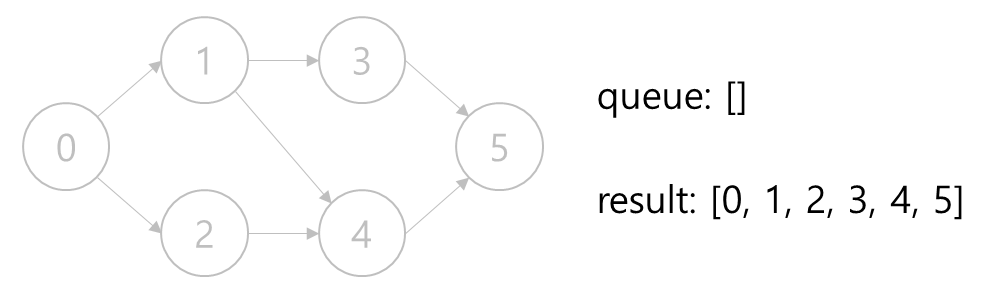
# 구현
간선을 제거한다는 동작은 노드의 수와 같은 길이를 가지는 진입 차수 배열을 만들고, 제거될 간선에 연결된 노드의 진입 차수 값을 줄이는 식으로 구현된다.
function topologySort(graph) {
const indegree = new Array(graph.length).fill(0);
// 진입 차수 정보 채우기
graph.forEach((edges) => {
edges.forEach((edge) => {
indegree[edge] += 1;
});
});
const result = [];
const queue = [];
// 진입 차수가 0인 노드를 찾아 큐에 추가
for (let i = 0; i < indegree.length; i += 1) {
if (indegree[i] === 0) {
queue.push(i);
}
}
// queue가 빌 때까지 반복
while (queue.length) {
let node = queue.shift();
result.push(node);
// 연결된 노드의 진입 차수 감소 (=== 연결된 간선 제거)
let connected = graph[node];
connected.forEach((conn) => {
indegree[conn] -= 1;
// 새롭게 진입 차수가 0이 된 노드를 큐에 추가
if (indegree[conn] === 0) {
queue.push(conn);
}
});
}
return result;
}
const graph = [[1, 2], [3, 4], [4], [5], [5], []];
console.log(topologySort(graph));
// Result: [1, 2, 3, 4, 5, 6]728x90
'Algorithms' 카테고리의 다른 글
| 누적 합 (feat. 파괴되지 않는 건물) - 2 (0) | 2023.09.05 |
|---|---|
| 누적 합 (feat. 파괴되지 않는 건물) - 1 (0) | 2023.09.05 |
| 크루스칼 알고리즘 (with JavaScript) (0) | 2023.09.02 |
| 서로소 집합 (with JavaScript) (0) | 2023.09.02 |
| 순열과 조합 (with JavaScript) (0) | 2023.08.24 |
