이제 문제를 풀어보자.
https://school.programmers.co.kr/learn/courses/30/lessons/92344
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
앞선 글에서 언급했듯이 brute force로 풀어서는 효율성 테스트를 통과하지 못한다.
이 문제를 푸는데 핵심이 되는 아이디어는 크게 2가지로,
1. 공격/회복을 전부 적용한 최종 결과를 한 번에 board에 적용한다. (공격/회복 하나씩 처리하면 안된다.)
2. 공격/회복 계산 시에는 역 누적합 배열을 이용한다.
1번은 쉽게 수긍이 되지만 2번은 저게 뭔 소린가 싶다.
이해를 위해 예를 들자면, 값이 모두 0인 배열에서 (1, 1) ~ (3, 3)까지의 값을 1씩 증가시킨다고 해보자.
단순 반복문으로 값을 갱신한다면 총 9개의 값을 바꿔주어야 한다.

여기서 이 원래의 배열을 다른 가상의 배열의 누적 합 배열이라고 생각해보자.
그리고 이 가상의 배열을 역 계산 해보면 아래와 같으며, 9개의 값을 갱신하는 작업을 4개의 값을 갱신하는 것으로 대체할 수 있음을 알 수 있다.
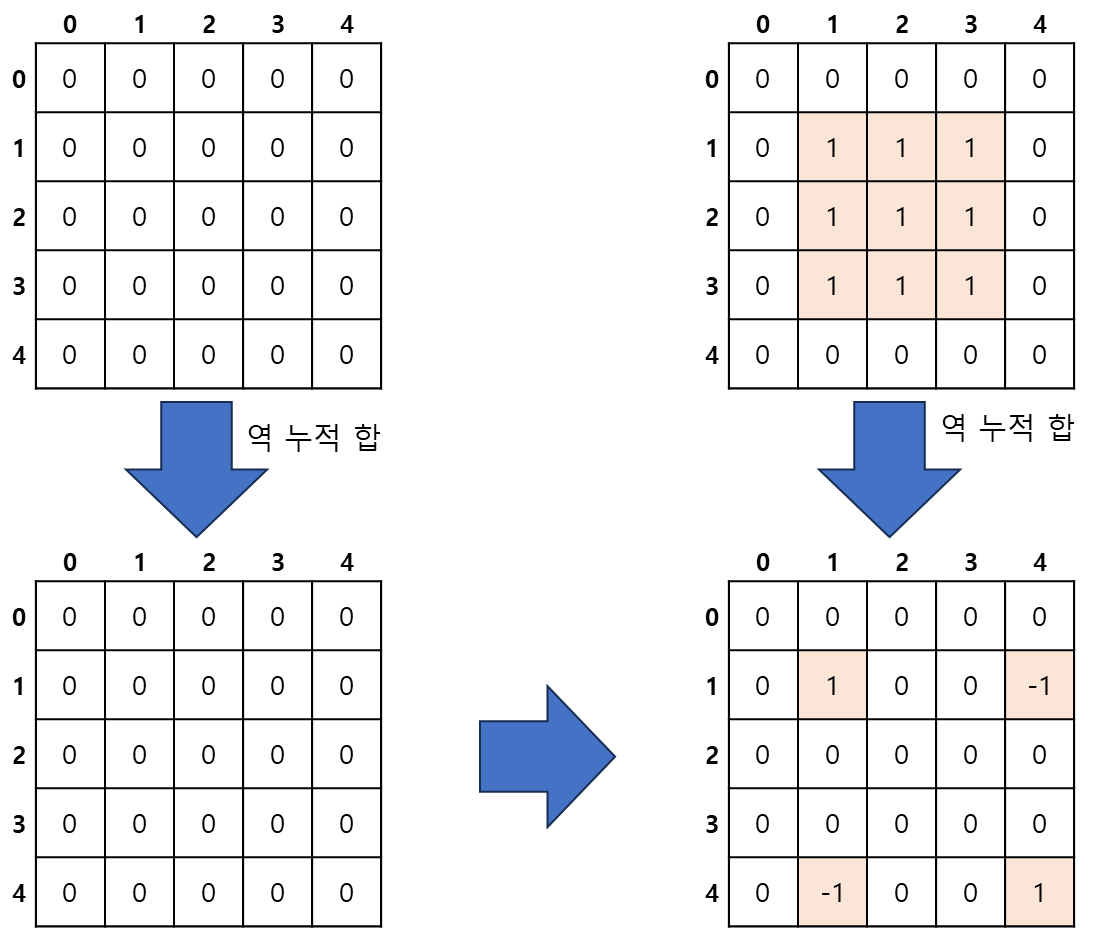
일반화 해보자.
(r1, c1) ~ (r2, c2)의 값을 degree만큼 증가시키고 싶으면 아래의 과정을 수행하면 된다.
- 역 누적 합 배열의 (r1, c1)의 값을 degree만큼 증가
- 역 누적 합 배열의 (r1, c2 + 1)의 값을 degree만큼 감소
- 역 누적 합 배열의 (r2 + 1, c1)의 값을 degree만큼 감소
- 역 누적 합 배열의 (r2 + 1, c2 + 1)의 값을 degree만큼 증가
이를 문제에 적용해서 코드를 작성하면 다음과 같다.
function solution(board, skill) {
let answer = 0;
// 역 누적 합 배열을 0으로 초기화
invSum = new Array(board.length + 1)
.fill()
.map(() => new Array(board[0].length + 1).fill(0)); // (*)
// 각각의 공격, 회복을 역 누적 합 배열에 적용
skill.forEach(sk => {
let [type, r1, c1, r2, c2, degree] = sk;
let sign = type === 1 ? -1 : 1;
invSum[r1][c1] += degree * sign;
invSum[r1][c2 + 1] -= degree * sign;
invSum[r2 + 1][c1] -= degree * sign;
invSum[r2 + 1][c2 + 1] += degree * sign;
});
// 역 누적 합 배열을 원래 배열로 변환
let diff = new Array(board.length)
.fill()
.map(() => new Array(board[0].length).fill(0));
for (let r = 0; r < board.length; r += 1) {
for (let c = 0; c < board[0].length; c += 1) {
diff[r][c] = invSum[r][c] +
(r > 0 ? diff[r-1][c] : 0) +
(c > 0 ? diff[r][c-1] : 0) -
(r > 0 && c > 0 ? diff[r-1][c-1] : 0);
if (board[r][c] + diff[r][c] > 0) answer += 1; // (**)
}
}
return answer;
}(*) : 역 누적 합 배열의 행, 열 크기를 원래 board의 크기보다 1씩 크게 설정하였다. 이는 값을 업데이트 할 때 'r2 + 1', 'c2 + 1'이 배열 크기보다 커지는 것을 방지하기 위함이다.
(**) : 반환 값은 최종 값이 0보다 큰 빌딩의 개수를 반환해주는 것이므로 원래 값 + skill에의한 diff 값이 0보다 큰 개수를 카운팅하였다.
'Algorithms' 카테고리의 다른 글
| Kadene's algorithm (1) | 2024.02.05 |
|---|---|
| Binary Search Tree (with JavaScript) (0) | 2023.09.09 |
| 누적 합 (feat. 파괴되지 않는 건물) - 1 (0) | 2023.09.05 |
| 위상 정렬 (with JavaScript) (0) | 2023.09.02 |
| 크루스칼 알고리즘 (with JavaScript) (0) | 2023.09.02 |
