# Binary Search Tree
번역하자면 이진탐색트리이며 줄여서 BST라고 부른다.
BST는 말 그대로 binary search를 더 효율적으로 하기 위한 트리 자료 구조이다.
삽입, 삭제, 조회의 시간 복잡도는 모두 O(log n)이다.
BST의 특징
1. 각 노드는 0 ~ 2개의 child node를 가진다.
2. 노드의 왼쪽 서브 트리의 값들은 항상 노드보다 작다.
3. 노드의 오른쪽 서브 트리의 값들은 항상 노드보다 크다.
4. 트리 내 중복되는 값은 없다.
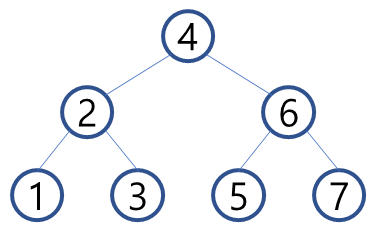
삽입
삽입할 값을 root node부터 순차적으로 비교하며 삽입 값이 더 작은 경우에는 왼쪽, 큰 경우에는 오른쪽으로 이동한다.
이동 중 빈 자리를 발견하면 그 곳에 삽입한다.
아래 트리에 '3'을 삽입한다고 해보자.
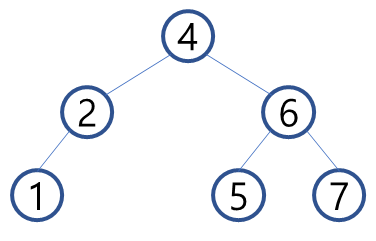
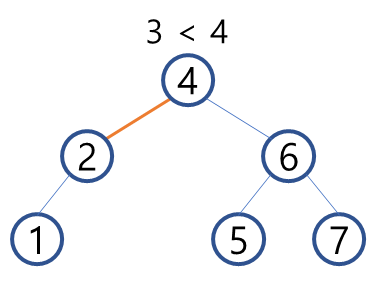
1. root node인 4와 비교하여 작으므로 왼쪽으로 이동한다.
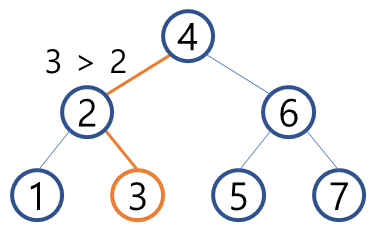
2. '2' node와 비교하여 크므로 오른쪽으로 이동한다. 이 때 오른쪽 자리가 비어있으므로 삽입한다.
삭제
1. Leaf node인 경우
해당 노드만 삭제하면 된다.
ex. Leaf node인 '3'을 삭제하는 경우
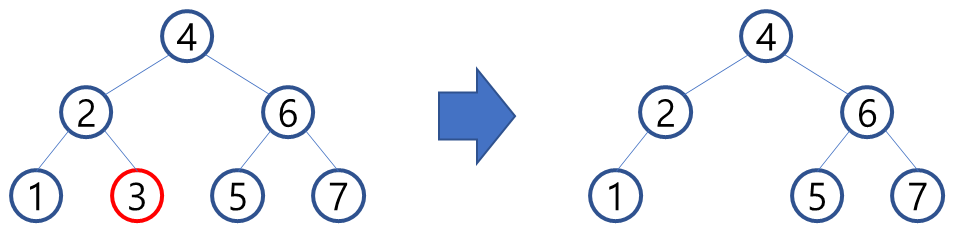
2. child node가 하나인 경우
노드를 삭제하고 child를 자신의 부모와 연결한다.
ex. Child가 하나인 node '2'를 삭제하는 경우

3. child node가 2개인 경우
노드를 삭제하고 child 중 중간 값을 가지는 노드를 삭제된 자리로 옮겨준다.
중간 값을 찾는 방법으로는 왼쪽 서브트리의 가장 큰 값을 선택하는 방법과 오른쪽 서브트리의 가장 작은 값을 선택하는 방법이 있다.
ex1. Node '4'를 삭제하고 왼쪽 서브트리의 가장 큰 값 선택
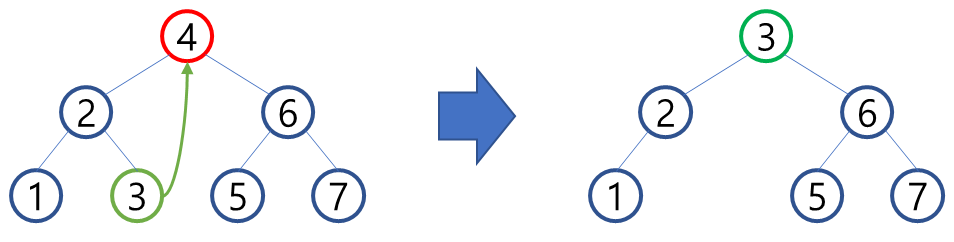
ex2. Node '4'를 삭제하고 오른쪽 서브트리의 가장 작은 값 선택
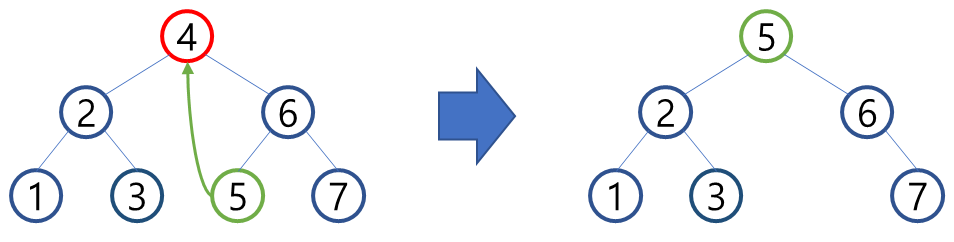
순회
순회는 기본적으로 트리의 왼쪽에서 오른쪽으로 진행된다.
이 때 root의 순서가 left, right와 비교했을 때 어디에 위치하느냐에 따라 전위, 중위, 후위 세 가지 종류로 나뉘게 된다.
아래 트리를 순회할 때 각 순회의 순서를 알아보자.
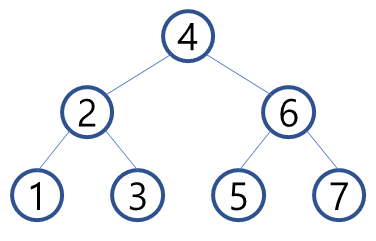
전위 순회 (preorder)
root를 첫 순서로 순회한다. (root -> left -> right)
순서: 4 -> 2 -> 1 -> 3 -> 6 -> 5 -> 7
중위 순회 (inorder)
root를 중간 순서로 순회한다. (left -> root -> right)
순서: 1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7
후위 순회 (postorder)
root를 마지막 순서로 순회한다. (left -> right -> root)
순서: 1 -> 3 -> 2 -> 5 -> 7 -> 6 -> 4
# 구현
먼저 Node class와 BinarySearchTree class가 필요하다.
Node는 value, left, right를 가지고 있으며
BinarySearchTree는 root node와 insert, delete, contains 등의 method를 가지고 있다.
Node & BinarySearchTree class
Node는 자신의 value와 left, right를 가진다. left, right는 Node | null이다.
BinarySearchTree는 root Node를 가지고 있으며, tree와 관련된 다양한 method를 가진다.
class Node {
constructor(value) {
this.value = value;
this.left = null;
this.right = null;
}
}
class BinarySearchTree {
constructor() {
this.root = null;
}
// methods below
// ...
}Insert
class BinarySearchTree {
// ...
insert(value) {
const newNode = new Node(value);
// 트리가 비어있으면 root로 설정
if (!this.root) {
this.root = newNode;
return this;
}
// 트리 상에서 위치 찾아 삽입
let current = this.root;
while (current) {
if (value < current.value) {
// 새 value가 current 보다 작은 경우 왼쪽에 삽입
if (current.left) {
current = current.left;
} else {
current.left = newNode;
}
} else if (value > current.value) {
// 새 value가 current 보다 큰 경우 오른쪽에 삽입
if (current.right) {
current = current.right;
} else {
current.right = newNode;
}
} else {
// 중복된 값인 경우 무시
return undefined;
}
}
}
// ...
}Delete
삭제할 노드의 left, right가 모두 있는 경우 오른쪽 subtree에서 대체 노드를 찾는 방식으로 구현하였다.
class BinarySearchTree {
// ...
delete(value) {
if (!this.root) return;
const deleteNode = (value, node) => {
if (node === null) return null;
// 지울 노드 탐색
if (value < node.value) {
node.left = deleteNode(value, node.left);
return node;
}
if (value > node.value) {
node.right = deleteNode(value, node.right);
return node;
}
// 지울 노드를 찾은 경우
// leaf node인 경우
if (!node.left && !node.right) {
return null;
}
// child가 하나인 경우
if (!node.left && node.right) {
return node.right;
} else if (node.left && !node.right) {
return node.left;
}
// child가 2개인 경우 (오른쪽 subtree의 가장 작은 값 선택)
let succ = node.right;
while (succ.left) {
succ = succ.left;
}
node.value = succ.value;
node.right = deleteNode(succ.value, node.right);
return node;
};
this.root = deleteNode(value, this.root);
}
// ...
}Transverse
세 종류 모두 기본적인 코드 구조는 같으나 callback 실행 시점이 다르다는 점을 주목하자.
class BinarySearchTree {
// ...
preorder(callback) {
const transverse = (node, callback) => {
if (!node) return;
callback(node);
transverse(node.left, callback);
transverse(node.right, callback);
};
transverse(this.root, callback);
}
inorder(callback) {
const transverse = (node, callback) => {
if (!node) return;
transverse(node.left, callback);
callback(node);
transverse(node.right, callback);
};
transverse(this.root, callback);
}
postorder(callback) {
const transverse = (node, callback) => {
if (!node) return;
transverse(node.left, callback);
transverse(node.right, callback);
callback(node);
};
transverse(this.root, callback);
}
// ...
}Others
BST가 특정 값을 가지고 있는지 확인하는 contain method.
class BinarySearchTree {
// ...
contains(value) {
let current = this.root;
let found = false;
while (current) {
if (value === current.value) {
found = true;
break;
} else if (value < current.value) {
current = current.left;
} else {
current = current.right;
}
}
return found;
}
// ...
}BST를 console에 출력하는 print method.
트리를 반시계 방향으로 90도 회전한 형태로 출력된다.
테스트 결과를 확인하기 위해 만들었다.
class BinarySearchTree {
// ...
print(node, depth) {
if (!node && !depth) {
node = this.root;
depth = 0;
} else if (!node || !depth) {
return;
}
this.print(node.right, depth + 1);
console.log(' '.repeat(depth) + String(node.value));
this.print(node.left, depth + 1);
}
// ...
}
# Test
Insert
- 테스트 코드
// binary search tree 생성
let bst = new BinarySearchTree();
bst.insert(4);
bst.insert(6);
bst.insert(2);
bst.insert(1);
bst.insert(5);
bst.insert(3);
bst.insert(7);
bst.print();
console.log('----------');- 예상 결과

- 실행 결과

Delete
- 테스트 코드
// ...
// node 3 삭제
bst.delete(3);
bst.print();
console.log('----------');
// node 2 삭제
bst.delete(2);
bst.print();
console.log('----------');
// 원상복구
bst = new BinarySearchTree();
bst.insert(4);
bst.insert(6);
bst.insert(2);
bst.insert(1);
bst.insert(5);
bst.insert(3);
bst.insert(7);
// node 4 삭제
bst.delete(4);
bst.print();
console.log('----------');- 예상 결과



- 실행 결과

Transverse
- 테스트 코드
// ...
// 원상복구
bst = new BinarySearchTree();
bst.insert(4);
bst.insert(6);
bst.insert(2);
bst.insert(1);
bst.insert(5);
bst.insert(3);
bst.insert(7);
// preorder transverse
let result = [];
bst.preorder((node) => {
result.push(node.value);
});
console.log(`preorder: ${result}`);
// inorder transverse
result = [];
bst.inorder((node) => {
result.push(node.value);
});
console.log(`inorder: ${result}`);
// postorder transverse
result = [];
bst.postorder((node) => {
result.push(node.value);
});
console.log(`postorder: ${result}`);- 예상 결과
preorder : 4 -> 2 -> 1 -> 3 -> 6 -> 5 -> 7
inorder : 1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7
postorder : 1 -> 3 -> 2 -> 5 -> 7 -> 6 -> 4
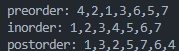
- 실행 결과
'Algorithms' 카테고리의 다른 글
| Levenshtein distance (1) | 2024.02.09 |
|---|---|
| Kadene's algorithm (1) | 2024.02.05 |
| 누적 합 (feat. 파괴되지 않는 건물) - 2 (0) | 2023.09.05 |
| 누적 합 (feat. 파괴되지 않는 건물) - 1 (0) | 2023.09.05 |
| 위상 정렬 (with JavaScript) (0) | 2023.09.02 |
