https://school.programmers.co.kr/learn/courses/30/lessons/92344
위 문제를 풀어보려다 보니 brute force로 풀면 정확도까지는 쉽게 통과가 되나 1,000 x 1,000 2차원 배열에 250,000개의 배열 업데이트를 해야 하니 효율성 테스트를 통과할 여지가 없다.
해설을 찾아보니 누적 합을 사용해서 풀어야 한다는데, 이번 기회에 해당 내용을 정리하고 문제 풀이를 해보려 한다.
# 1차원 누적 합
1차원 배열에서의 누적 합을 구하는 함수를 'f(x)'라 할 때 다음과 같이 정의된다. (구현 시 편의 상 i = 0부터 시작하는 것으로 하였다.)
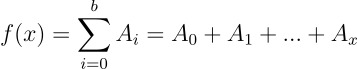
이 때 x = a에서 x = b까지의 부분합을 구하고 싶다면, 다음과 같이 나타낼 수 있다.
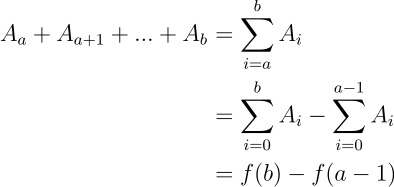
이를 JavaScript로 구현하면 f(x)의 결과값을 저장하는 배열을 만들고, b번째 값에서 a-1번째 값을 빼는 것으로 누적 합을 구할 수 있다.
// 원본 값
let arr = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9];
console.log(`Original: [${arr}]`);
// 누적 합 배열 생성
let prefixSum = new Array(arr.length);
prefixSum[0] = arr[0];
for (let i = 0; i < arr.length; i += 1) {
prefixSum[i] = arr[i] + (i > 0 ? prefixSum[i - 1] : 0);
}
console.log(`PrefixSum: [${prefixSum}]`);
// a ~ b 까지 누적 합 계산
let a = 3;
let b = 6;
let result = prefixSum[b] - prefixSum[a - 1];
console.log(`Sum ${a} ~ ${b}: ${result}`);
# 2차원 누적 합
2차원 배열로 확장하면 정의가 다음과 같이 바뀐다.
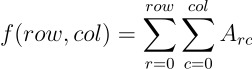
2차원부터는 그림으로 이해하는 편이 쉽다.
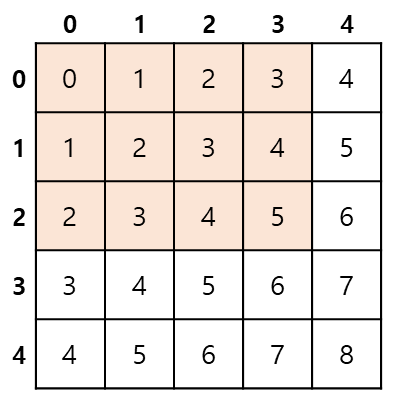
다음과 같은 2차원이 있다고 하자.
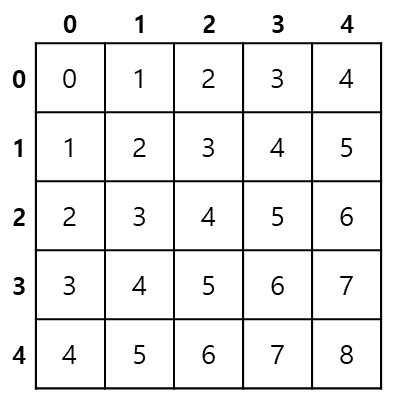
이 때 f(2, 3)은 아래 색칠된 영역의 값을 더한 30이다.
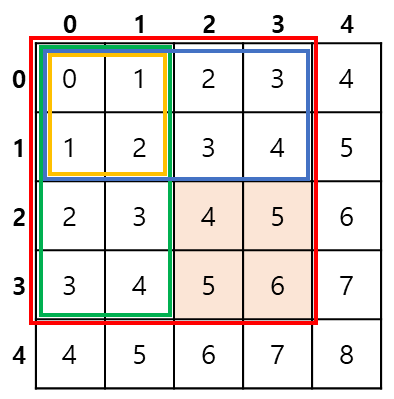
만약 (2, 2)에서 (3, 3)까지의 누적 합을 구한다고 한다면,
빨간 영역인 f(3, 3) 에서
녹색 영역 f(3, 1) 과 파란색 영역 f(1, 3) 을 빼주고
중복으로 빠진 노란색 영역 f(1,1)을 다시 더해주면 된다.
따라서 (r1, c1) ~ (r2, c2)의 부분합을 수식으로 나타내보면 다음과 같다.
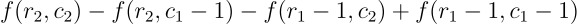
이를 JavaScript로 구현해보자.
// 원본 값
let arr = [
[0, 1, 2, 3, 4],
[1, 2, 3, 4, 5],
[2, 3, 4, 5, 6],
[3, 4, 5, 6, 7],
[4, 5, 6, 7, 8],
];
console.log('Original:');
console.log(arr);
// 누적 합 배열 생성
let prefixSum = new Array(arr.length)
.fill()
.map(() => new Array(arr[0].length).fill());
for (let r = 0; r < arr.length; r += 1) {
for (let c = 0; c < arr[0].length; c += 1) {
prefixSum[r][c] =
arr[r][c] +
(r > 0 ? prefixSum[r - 1][c] : 0) +
(c > 0 ? prefixSum[r][c - 1] : 0) -
(r > 0 && c > 0 ? prefixSum[r - 1][c - 1] : 0);
}
}
console.log('PrefixSum:');
console.log(prefixSum);
// (r1, c1) ~ (r2, c2) 까지 누적 합 계산
let r1 = 2;
let c1 = 2;
let r2 = 3;
let c2 = 3;
let result =
prefixSum[r2][c2] -
prefixSum[r1 - 1][c2] -
prefixSum[r2][c1 - 1] +
prefixSum[r1 - 1][c1 - 1];
console.log(`Sum (${r1}, ${c1}) ~ (${r2}, ${c2}): ${result}`);
이미 글이 꽤나 길어져버려서 처음 제시되었던 문제의 풀이는 다음 글에 이어서 작성하겠다.
'Algorithms' 카테고리의 다른 글
| Binary Search Tree (with JavaScript) (0) | 2023.09.09 |
|---|---|
| 누적 합 (feat. 파괴되지 않는 건물) - 2 (0) | 2023.09.05 |
| 위상 정렬 (with JavaScript) (0) | 2023.09.02 |
| 크루스칼 알고리즘 (with JavaScript) (0) | 2023.09.02 |
| 서로소 집합 (with JavaScript) (0) | 2023.09.02 |
